F2 RE-APPORTIONMENT OF SERVICE COST CENTRE COSTS (2)

来源: 编辑： 2013/11/04 15:13:43　字体：大小

THE RECIPROCAL METHOD

This approach is used where some service cost centres provide services to other service cost centres, and the service is reciprocated. In Example 3, cost centre C serves centre D, and vice versa. In reality, an organisation may choose to ignore this reciprocal service and re-apportion overheads by using the direct or step down approach. In Example 3, the direct approach would involve re-apportioning C’s overhead on the basis of 40/90 and 50/90 to A and B respectively and ignoring the reciprocal service to D. D’s overheads would be similarly reapportioned on the basis of 75/95 and 20/95.

However, if we choose to fully reflect the reciprocal services between C and D, one of two methods are possible – the repeated distribution approach or the algebraic approach. Both are methods of solving a simultaneous equation and should give the same result. Example 3 demonstrates both methods. In the exam, the examiner will indicate that he wants you to use one or either of these methods by asking for a method that ‘fully reflects the reciprocal services involved’. Practically in the Paper F2 exam, where this topic would be examined by two-mark questions, the focus will be on the algebraic approach as repeated distribution would be too time consuming.

Example 3

Data as Example 1 apart from usage of C and D’s services has again changed. Usage of service cost centres is as follows:

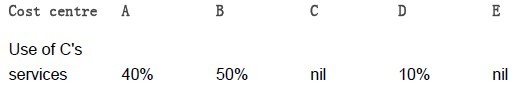
REPEATED DISTRIBUTION APPROACH

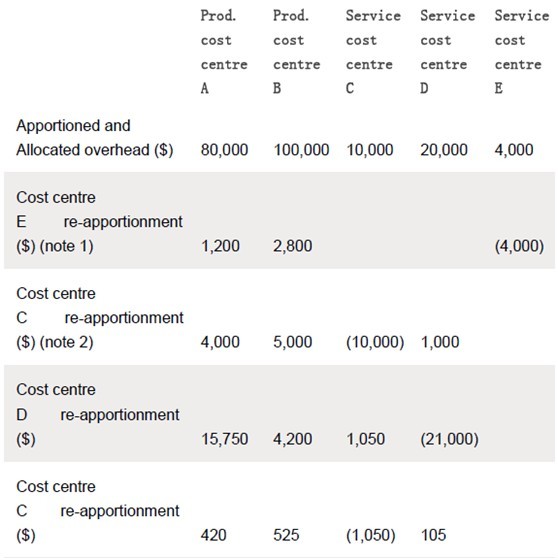
Note 1 E’s costs are apportioned directly as no reciprocal service is involved.

Note 2 It doesn’t really matter which of the two remaining cost centres you start with. Note 3 On the last reapportionment, D’s overheads are apportioned on the basis of 75/95 to A and 20/95 to B. The reciprocal service to C is ignored as, by now, it is not material.

ALGEBRAIC APPROACH

Firstly, we can setup the overhead re-apportionment process as a set of equations.

Let:

A = the total overhead $ apportioned to department A

B = the total overhead $ apportioned to department B, etc

Then:

A = 80,000 + 0.40 C + 0.75 D + 0.30 E

B = 100,000 + 0.50 C + 0.20 D + 0.70 E

C = 10,000 + 0.05 D

D = 20,000 + 0.10 C E = 4,000

If you remember your school maths, you will note that the equations for C and D are simultaneous – ie C is a function of D, and D is a function of C. These two equations must be solved first. Various approaches are possible to solve simultaneous equations but substitution is probably quickest.

Substituting the D equation into the C equation:

C = 10,000 + 0.05 (20,000 + 0.10 C)

Multiplying out the bracket:

C = 10,000 + 1000 + 0.005 C

Collecting terms:

0.995 C = 11,000

C = 11,055.3

Substituting into the D equation:

D = 20,000 + 0.10 × 11,055.3

D = 21,105.5

Finally, plugging these values into the equations for A and B, the total overhead apportioned to each of the production cost centres is:

A = 80,000 + 0.40 × 11,055.3 + 0.75 × 21,105.5 + 0.3 × 4,000

A = 101,451.2

B = 100,000 + 0.50 × 11,055.3 + 0.20 × 21,105.5 + 0.7 × 4,000

B = 112, 548.8

These results, as they should be, are quite close to the repeated distribution approach.

TEST YOUR UNDERSTANDING

The following question is representative of questions on this topic that you might experience in the Paper F2 exam.

A company has two production cost centres (V and W) and two service cost centres (X and Y). The following overheads have been apportioned and allocated to the four cost centres.

How much would cost centre V’s total overhead cost be if the company used the step-down approach to re-apportion service cost centre overhead?

A $10,400

B $10,720

C $16,400

D $16,720

The correct answer is D ($6,000 + $4,000 × 0.6 + 0.8 × ($10,000 + 0.1 × $4,000))

Written by a member of the Paper F2/FMA examining team

Page1>> The original article>>