扫码下载APP
及时接收最新考试资讯及
备考信息
为帮助大家对中级《审计专业相关知识》的学习,小编为大家整理了正保会计网校2020年中级《审计专业相关知识》辅导班老师讲解的讲义内容。
下文为2020年中级《审计专业相关知识》第二部分第一章第二节的知识点,还未开始2021年中级审计师考试备考的同学可参考以下内容,提前学习,其他章节内容小编将为大家陆续更新,请大家持续关注!

第二节 货币时间价值
知识点:货币时间价值的含义及基本原理
1.货币时间价值
货币资本经过一定时间的投资和再投资所增加的价值,也称资本时间价值、现金流量时间价值。
2.货币时间价值的应用
(1)现值:把不同时间的货币价值折算到当前时点,然后对其现值进行运算和比较。
(2)早收晚付:对于不附带利息的收支,与其晚收不如早收,与其早付不如晚付。
3.货币时间价值计算先导知识
(1)时间轴
时间轴以0为起点(表示现在),每一个点代表该期的期末及下期的期初。
(2)终值与现值
| 终值(F) | 将来值,是现在一定量的货币按照某一收益率折算到未来某一时点所对应的金额,例如:本利和 |
| 现值(P) | 未来某一时点上一定量的货币按照某一收益率(折现率)折算到现在所对应的金额,例如:本金、证券价值 |
知识点:复利终值与现值——一次性款项的终值与现值
1.复利终值(一次性款项的终值):本金按复利计息若干期后的本金与利息之和。即:已知现值P(现在的一次性款项)、利率i、期数n(终值与现值之间的间隔期),求终值F。

F=P×(1+i)n=P×(F/P,i,n)
【示例】
某企业将50000元存入银行,年利率为5%,该笔存款在5年后复利终值可计算如下:
F=50000×(1+5%)5≈63814(元)
=50000×(F/P,5%,5)=50000×1.276=63800(元)
2.复利现值(一次性款项的现值):未来货币按复利计算的现在价值,是复利终值的逆运算。即:已知终值F(未来某一时点上的一次性款项)、利率i、期数n(终值与现值之间的间隔期),求现值P。

P=F×(1+i)-n=F×(P/F,i,n)
【提示】
复利终值与复利现值互为逆运算,复利终值系数(1+i)n与复利现值系数(1+i)-n之间互为倒数。
【示例】
某企业计划4年后需要150000元用于研发,当银行存款年利率为5%时,按复利计息,则现在应存入银行的本金可计算如下:
P=150000×(P/F,5%,4)=150000×0.823=123450(元)
知识点:年金终值与现值——系列、定期、等额款项的复利终值或现值的合计数
1.年金:等额、定期的系列收支
(1)系列——通常是指多笔款项,而不是一次性款项
(2)定期——每间隔相等时间(未必是1年)发生一次
(3)等额——每次发生额相等
【提示】
对于符合年金形态的系列款项,可利用等比数列求和的方法计算其终值或现值的合计数,而无需逐一计算每一笔款项的终值或现值,然后再加总。
【示例】
年金形式系列款项的终值合计与现值合计:

2.普通年金终值与现值
(1)普通年金(后付年金):从第一期起,各期期末收付的年金

①n期内共发生n笔年金(n个A);
②第1笔年金发生在时点1(第一期期末),最后1笔年金发生在时点n(最后一期期末)。
(2)普通年金终值:一定时期内每期期末等额收付款项的复利终值之和。
即:已知年金A(系列定期等额款项的每笔发生额)、利率i、期数n(年金A的个数),求n个A的终值合计F。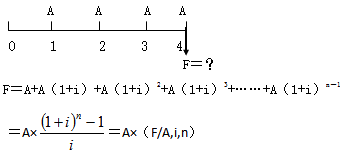
【示例】
某企业在年初计划未来5年每年底将50000元存入银行,存款年利率为5%,则第5年底该年金的终值可计算如下:
F=50000×(F/A,5%,5)=50000×5.526=276300(元)
(3)普通年金现值:一定时期内每期期末等额收付款项的复利现值之和。即:已知年金A(系列定期等额款项的每笔发生额)、利率i、期数n(年金A的个数),求n个A的现值合计P。 
【示例】
某企业年初存入银行一笔款项,计划用于未来5年每年年底发放职工养老金80000元,若存款年利率为6%,则现在应存入的款项可计算如下:
P=80000×(P/A,6%,5)=80000×4.212=336960(元)
第03讲 预付年金终值与现值、递延年金现值、永续年金现值
3.预付年金终值与现值
(1)预付年金(即付年金、期初年金):从第一期起,各期期初收付的年金

①n期内共发生n笔年金(n个A);
②第1笔年金发生在时点0(第一期期初),最后1笔年金发生在时点n-1(最后一期期初)。
【提示】
在期数相同的情况下,普通年金与预付年金的年金个数相同(n期内有n笔年金);二者的区别仅在于收付款时间的不同:普通年金发生于各期期末(1~n),在0时点(第一期期初)没有发生额;预付年金发生于各期期初(0~n-1),在n时点(最后一期期末)没有发生额。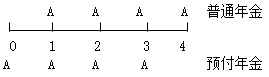
(2)预付年金终值:由于预付年金的每一笔年金都比普通年金提前一期发生,因而在计算终值时,预付年金的每一笔年金都要比普通年金多一个计息期。

预付年金终值=普通年金终值×(1+i)

即:预付年金终值系数是在普通年金终值系数基础上,期数加1,系数减1的结果。
【示例】
某公司打算购买一台设备,付款方式为每年初支付200万元,3年付讫。假设年利率为5%,复利计息。则该公司购置设备的付款额终值为:
F=200×(F/A,5%,3)×(1+5%)=200×[(F/A,5%,4)-1]=662.02(万元)
(3)预付年金现值:由于预付年金的每一笔年金都比普通年金提前一期发生,因而在计算现值时,预付年金的每一笔年金都要比普通年金少折现一期。

预付年金现值=普通年金现值×(1+i)
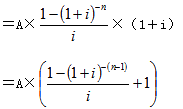
=A×[(P/A,i,n-1)+1 ]
即:预付年金现值系数是在普通年金现值系数基础上,期数减1,系数加1的结果。
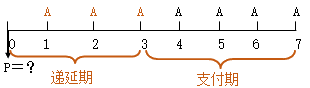
4.递延年金现值
(1)递延年金(延期年金):不是从第一期开始,而是若干期后才开始发生的每期期末等额收付款项。

递延期=第一笔年金发生的期末数-1
支付期=年金A的个数
(2)递延年金现值的计算
①分段折现法
在递延期末或支付期初(第一笔年金发生的前一个时点)将时间轴分成两段。

先计算支付期的普通年金现值(P′),即支付期内各期年金在支付期初或递延期末(第一笔年金发生的前一个时点)的现值合计,再计算P′在递延期初的复利现值。

②插补法
假设递延期内也有年金发生,先计算“递延期+支付期”的年金现值,再扣除递延期内实际并未发生的年金现值。
P=A×[(P/A,i,递延期+支付期)-(P/A,i,递延期)]
5.永续年金现值
(1)永续年金(永久年金):无限期收付款项的年金

【提示】永续年金没有到期日,因而没有终值。
(2)永续年金现值=A/i
【示例】
某种永续年金每年收款1200元,折现率为10%,则该永续年金的现值可近似地计算为:P=1200/10%=12000(元)
以上内容均来自正保会计网校2020年审计师辅导班老师讲解内容,成为付费学员就可查看更多讲义、习题与课程!网校老师帮你抓重点、提炼考点!快去入手吧!立即购买>>
相关阅读:
点击图片查看课程↓↓
推荐阅读:
Copyright © 2000 - www.fawtography.com All Rights Reserved. 北京正保会计科技有限公司 版权所有
京B2-20200959 京ICP备20012371号-7 出版物经营许可证 ![]() 京公网安备 11010802044457号
京公网安备 11010802044457号